Binary trees
Oscar David Porras Orjuela - 854046
Juan Sebastian Barrera Lasprilla - 833481
Introduction
Binary trees are fundamental data structures in computer science, widely used for organizing and manipulating hierarchical data.
we are going to show you the basic concepts of binary trees and how implementat it in Java.
What are Binary Trees?
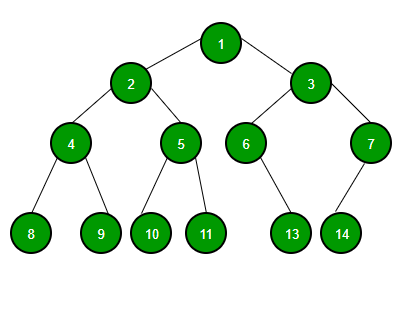
It is a tree-like data structure consisting of nodes, where each node can have at most two child nodes, referred to as the left child and the right child.
The topmost node in a binary tree is known as the root. Nodes in a binary tree can be connected in a way that reflects a hierarchical relationship, making it an efficient choice for organizing data that has a parent-child association.
Glossary
Node: Each element in a binary tree is called a node. It contains data and pointers to its left and right child nodes.
Root: The topmost node of a binary tree is referred to as the root.
Leaf Node: Nodes that do not have any child nodes.
Parent Node: A node that has one or more child nodes.
Child Node: Nodes that are connected to a parent node.
Depth (Level) : The depth of a node in a binary tree represents the number of edges between the root and that node.
Height: The height of a binary tree is the maximum depth among all its nodes.
Binary Tree Operations:
Insertion: Adding a new node to the binary tree.
Search: Finding a specific value within the binary tree.
Deletion: Removing a node from the binary tree.
Traversal: Visiting nodes in a specific order, such as in-order, pre-order, or post-order traversal.
1) In-order Traversal:
In in-order traversal, the left subtree is visited first, followed by the root node, and then the right subtree. This traversal order produces the nodes of the binary tree in ascending order when applied to a binary search tree.
The general algorithm for in-order traversal is as follows:
• Traverse the left subtree recursively.
• Visit the root node.
• Traverse the right subtree recursively.
2) Pre-order Traversal:
In pre-order traversal, the root node is visited first, followed by the left subtree, and then the right subtree. This traversal order is useful for making a copy of the tree, as it creates a copy that is structurally identical to the original tree.
The general algorithm for pre-order traversal is as follows:
• Visit the root node.
• Traverse the left subtree recursively.
• Traverse the right subtree recursively.
3) Post-order Traversal:
In post-order traversal, the left subtree is visited first, followed by the right subtree, and then the root node. This traversal order is often used in deleting or freeing nodes from a binary tree.
The general algorithm for post-order traversal is as follows:
• Traverse the left subtree recursively.
• Traverse the right subtree recursively.
• Visit the root node.
Videos to reforce the information and how implement binary trees in java: